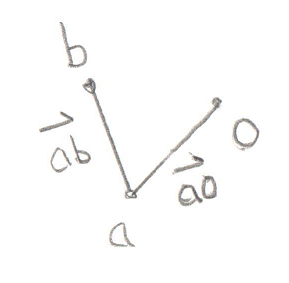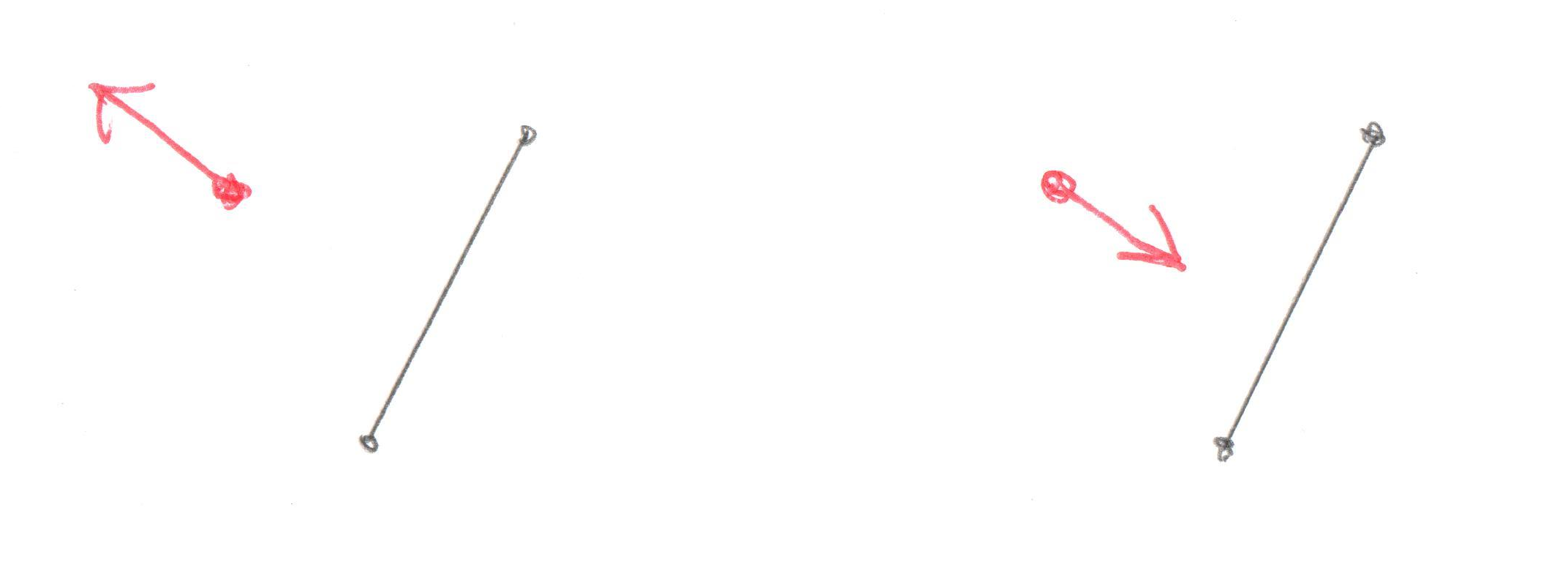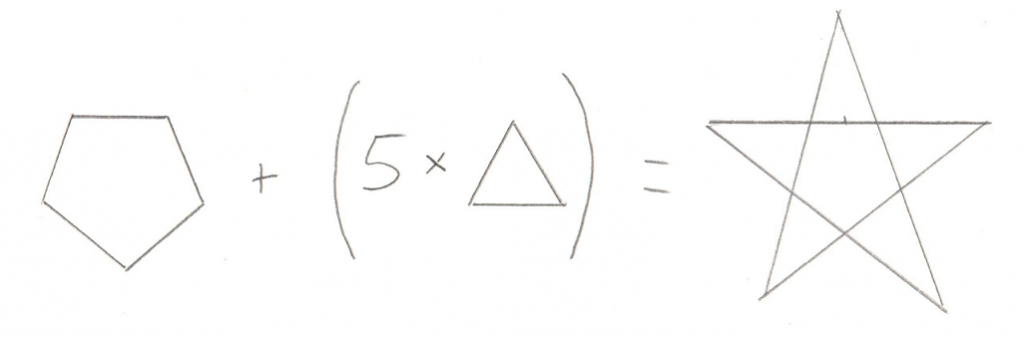Welcome to the final post on implementing the GJK. In the first post, we looked at some of the basics and described the algorithm in general terms. In the second post we looked at how the GJK is set up in the Dubious Engine. In this post we’re going to dig down into the lowest layer, where we build and maintain the Minkowski Simplex.
Let me set the stage from our last post. We were in a loop, trying to find a new Support Point and Support Vector. If a suitable candidate was found, the loop would end like this (not really, but close, the real code is here)
simplex.push_back( support_point);
bool collision_found = simplex.build();
if (collision_found) {
return true;
}
So we’re going to be looking at the Minkowski_simplex in detail. Internally it basically holds 4 points (the code is a little bit more complicated for efficiency’s sake). Why 4 points? Remember that in 3D a simplex is a tetrahedron, which is a shape made of 4 points. Not all 4 points are in use at all times. The algorithm starts with a simple Line (ie 2 points). When a new Support Point is added, the simplex becomes a Triangle. Then another new Support Point turns it into a Tetrahedron. If that is not found to contain the origin, then a point is dropped and the simplex becomes a Triangle again. Let’s take a look at how it works.
The Minkowski_simplex::push_back function is trivial. If it were implemented with an actual std::vector it would literally be a call to std::vector::push_back. But what’s up with the build function?
std::tuple<bool, Math::Vector>
Minkowski_simplex::build()
{
switch (m_size) {
case 2:
return build_2();
case 3:
return build_3();
case 4:
return build_4();
default:
throw std::runtime_error("Received simplex of incorrect size");
}
}
As you can see, there are only three valid point counts, corresponding to the Line, Triangle, and Tetrahedron.
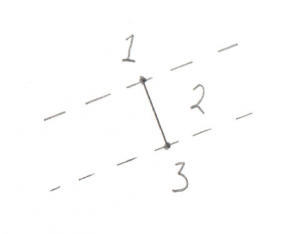
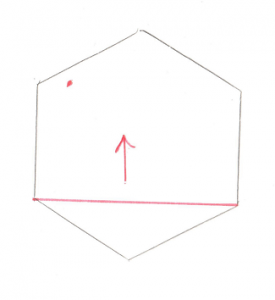
Test 1: Line
Given a simple Line of only two Points, this image shows the 3 possible areas where the origin could be:
- Past the end of the Line
- Between the two ends of the Line
- Past the other end of the Line
Hopefully that’s not too confusing. It turns out that there are actually less real possibilities. Recall in the previous post I devoted a lot of time to the dot_product test between the Support Point and Support Vector. I said it was “critically important.” The reason it’s so critical is that it lets us disregard areas 1 and 3 in the above image. This is because areas 1 and 3 correspond to a situation where the Support Point is out past the end of the Support Vector. And our dot_product test is done to look for exactly this situation, because if the Support Point is out past the end of the Support Vector then there’s no way the resulting simplex can contain the origin. To say it another way, the dot_product test has already filtered out areas 1 and 3, so we don’t even need to look for them. This makes the search for the origin in relation to this line very easy, the origin is either on one side or the other.
Let’s have a look at the code.
std::tuple<bool, Math::Vector>
Minkowski_simplex::build_2()
{
const Math::Vector& a = m_v[1].v();
const Math::Vector& b = m_v[0].v();
const Math::Vector origin;
const Math::Vector& ab = b - a;
const Math::Vector& ao = origin - a;
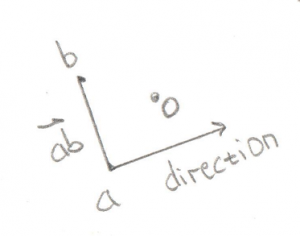
You’ll notice in all this code I try to name things consistently. Points in the simplex are a, b, c, and d, and the origin is o. A Vector pointing from a to b (counter-intuitively calculated by b-a) is called ab.
For this next bit I’m changing the real code by inserting a tmp Vector to make it a bit clearer
Math::Vector tmp = Math::cross_product(ab, ao);
Math::Vector direction = Math::cross_product( tmp, ab);
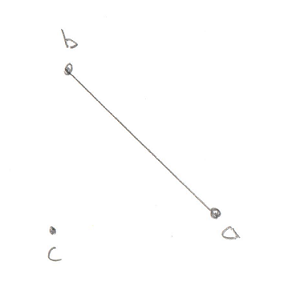
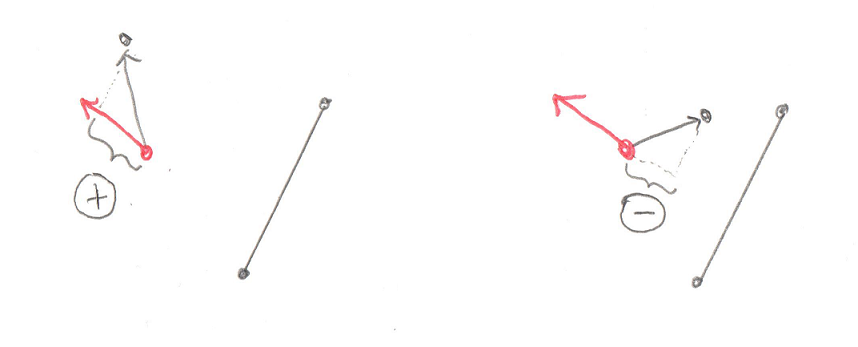
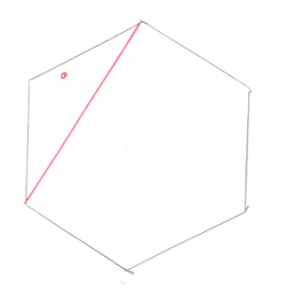
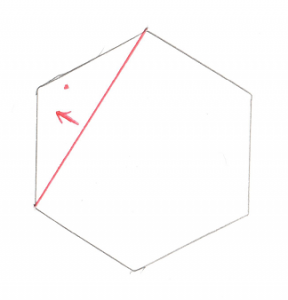
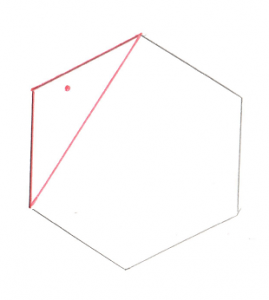
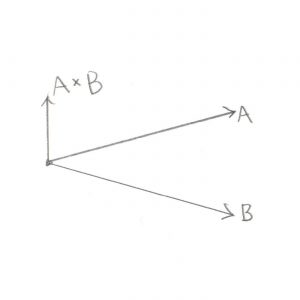
Okay, this is the important part of this test. Let’s look at what’s going on with these two Cross Products. What we’re trying to find is the direction of the origin. Let’s use this as an example, in this image we have Vectors ab and ao:
You’ll recall that a Cross Product of any two Vectors is a third Vector that is perpendicular to both of them. In this case the two Vectors both lie on the plane of your monitor, so the Cross Product of ab and ao, stored in tmp, is a new Vector that points directly out of your monitor and at you. Grab a pencil and stick the eraser on point a and point the tip at you, that’s the Vector tmp. The next part of the code takes the Cross Product of tmp and ab. That would be a new Vector that’s perpendicular to ab and points in the direction of the origin.
Pretty cool, huh? By using two Cross Products we’ve found the direction Vector we’re looking for. That will become the new Support Vector for the next phase of the GJK.
But before we move ahead, there’s an edge case to worry about (there’s always an edge case).
if (direction == Math::Vector()) {
if (Math::equals(fabs(ao.y()), 0) &&
Math::equals(fabs(ao.x()), 0)) {
direction = Math::Vector(0, 1, 0);
}
else {
direction = Math::Vector(ao.y(), -ao.x(), 0);
}
}
return std::make_tuple(false, direction);
}
If the origin happens to fall exactly on the Vector ab, then the Cross Product will fail and we’ll be left with an empty direction Vector. In this case we can try to create a perpendicular Vector manually.
So that’s the code for the Line test. Not too bad I hope. The following tests are basically the same idea, but with more possible locations to look for the origin, and a few quirks to deal with.
Test 2: Triangle
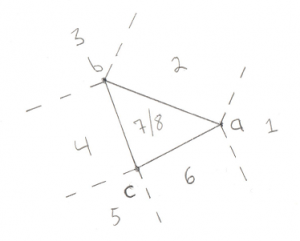
This one is a bit more complex, but it still breaks down into distinct places where the origin can be:
- Past Point A (not possible)
- Outside line AB
- Past Point B (not possible)
- Outside line BC (not possible)
- Past Point C (not possible)
- Outside line CA
- Above the triangle
- Below the triangle
We can eliminate cases 1, 3, and 5 due to the same optimization discussed for the Line test, if the origin was past the lines then we would give up before entering this test. We can also eliminate the outside of Vector bc. This is a bit of a surprise. This is because Vector bc turns out to be the Line we tested previously. In order to get to this stage we already know that the origin is on one side of Vector bc, so there’s no need to test the other side. What’s left is 2 Line tests (cases 2 and 6) and 2 Triangle tests (cases 7 and 8).
Let’s look at some code:
std::tuple<bool, Math::Vector>
Minkowski_simplex::build_3()
{
const Math::Vector& a = m_v[2].v();
const Math::Vector& b = m_v[1].v();
const Math::Vector& c = m_v[0].v();
const Math::Vector origin;
const Math::Vector& ab = b - a;
const Math::Vector& ac = c - a;
const Math::Vector& ao = origin - a;
const Math::Vector& ab_x_ac = Math::cross_product(ab, ac);
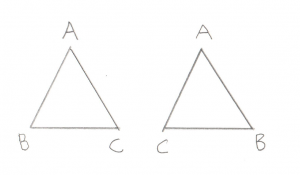
I discussed the naming of a, b, and c previously. It’s important to note that b and c are the same Points used in the above Line test. This is how we can exclude the test on the outside of bc. Vectors ab, ac, and ao are simply created by subtracting the points, same as last time. Vector ab_x_ac (pronounced “ab cross ac”) is the Triangle Normal, ie a Vector pointing perpendicular to the outside of the Triangle. Recall the discussion of the Winding Order, it’s very important that this Triangle is ABC and not ACB. You will see the code moving points around to make sure the winding remains consistent.
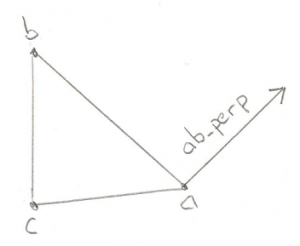
So what’s the plan of attack? For the lines tests (cases 2 and 6) we want to find a Vector that points away from an edge, and then test if the origin overlaps with that Vector. Let’s start with the ab edge:
const Math::Vector& ab_perp = Math::cross_product(ab, ab_x_ac);
if (Math::dot_product(ao, ab_perp) > 0) {
m_v[0] = m_v[1];
m_v[1] = m_v[2];
--m_size;
return std::make_tuple(false, ab_perp);
}
The Vector ab_perp is a Vector perpendicular to edge ab.
Again we can use the Cross Product to find a Vector perpendicular to any two Vectors, in this case edge ab and the Triangle Normal. We can take the dot product of this new Vector and the ao Vector to find out if ao is on the outside of the Triangle along ab_perp. If it is then we throw away point c and reduce our Minkowski Simplex to a simple Line, and return a new Support Vector to search in.
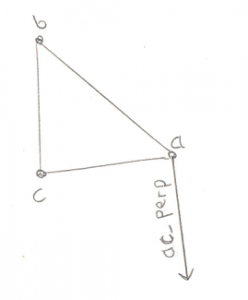
If that test fails then we want to do the exact same test, but this time along edge ac:
const Math::Vector& ac_perp = Math::cross_product(ab_x_ac, ac);
if (Math::dot_product(ao, ac_perp) > 0) {
m_v[1] = m_v[2];
--m_size;
return std::make_tuple(false, ac_perp);
}
If this test passes then the origin is outside of the triangle on the ac side.
This means we have to throw away point b.
If none of these tests find the origin then we can conclude that it’s not outside of any of the edges, so it must be inside the Triangle. So now it’s just a question of whether the origin is above the triangle, or below it.
float side_check = Math::dot_product(ab_x_ac, ao);
if (side_check > 0) {
return std::make_tuple(false, ab_x_ac);
}
The check to see if it’s above the triangle is trivial, just use the Dot Product to see if Vector ao is along the Triangle Normal. If it is then we retain our entire Triangle and return the new Support Vector.
Finally if it’s not above our Triangle, it must be below it (okay fine, or precisely on it but that edge case doesn’t need to be handled differently)
std::swap(m_v[0], m_v[1]);
return std::make_tuple(false, ab_x_ac * -1);
}
Wait wait, what’s going on with the call to std::swap? Remember I said that the Winding Order is important? For our Tetrahedron test we need to know which side of the Triangle the origin is on. I set it up so that it’s always on the “outside.” But in this case, the origin is “inside” the Triangle. So I fix this by simply flipping two points on the Triangle, thereby reversing the Winding Order and making the old “inside” the new “outside.” Cool trick, huh?
Test 3: Tetrahedron
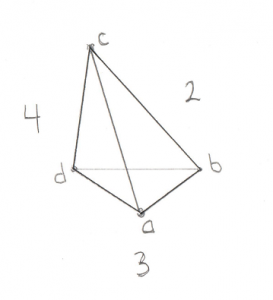
Hoo boy, the Tetrahedron! If you’re comfortable with the triangle case then this one isn’t a stretch of the imagination. It is, however, a stretch of my drawing abilities:
For this image assume Point a is closest to you. Here’s the places where the origin could be:
- Past any of the 4 points (not possible)
- Outside triangle ABC
- Outside triangle ADB
- Outside triangle ACD
- Outside triangle BDC (not possible)
- Inside the Tetrahedron
I compressed the 4 end point checks into case 1. As before, they’re not possible in our situation due to the Dot Product test that I’ve been harping on about. And just like for the Triangle case it wasn’t possible to be outside of the Line we started with, for the Tetrahedron it’s not possible to be outside of the Triangle we started with (case 5).
Then there are 3 remaining triangle tests. If it turns out that the origin is outside of one of these Triangles then we drop the Point at the opposite side and are left with just a Triangle. Then we define the Support Vector to be in the direction from this Triangle to the origin. We grab a new Point and are left with a new Tetrahedron and the tests begin again.
Let’s bring on the code:
std::tuple<bool, Math::Vector>
Minkowski_simplex::build_4()
{
const Math::Vector& a = m_v[3].v();
const Math::Vector& b = m_v[2].v();
const Math::Vector& c = m_v[1].v();
const Math::Vector& d = m_v[0].v();
const Math::Vector origin;
const Math::Vector& ab = b - a;
const Math::Vector& ac = c - a;
const Math::Vector& ad = d - a;
const Math::Vector& ao = origin - a;
This bit should look very familiar by now. Let’s be very specific about the Winding Order. You’ll remember from the Triangle test above that we left with the Support Vector on the “outside” of the triangle. Since the new point would have been pushed back to the last position in the array, this means that points b, c, and d define the Triangle we were looking at before. This also means that a is “outside” the Triangle, and that from a‘s perspective, b, c, and d are wound counter-clockwise.
Next we set up the usual edge Vectors, ab, ac, ad, and the Vector to the origin, ao. We don’t bother defining the other edges (bc, bd, or cd) because we already know the origin can’t be outside of that Triangle (case 5 above) so there’s no need.
Let’s have a look at the test outside of Triangle ABC (case 2):
const Math::Vector& ab_x_ac = Math::cross_product(ab, ac);
if (Math::dot_product(ab_x_ac, ao) > 0) {
m_v[0] = m_v[1];
m_v[1] = m_v[2];
m_v[2] = m_v[3];
--m_size;
return std::make_tuple(false, ab_x_ac);
}
The Vector ab_x_ac (pronounced “ab cross ac”) is the Normal to Triangle ABC. By checking the Dot Product of that Normal with the Vector to the origin we can see if the origin is outside Triangle ABC. If it is then Triangle ABC becomes our new starting Triangle and ab_x_ac becomes out new Support Vector. This means we drop point d as we know the origin is not on that side of the Tetrahedron. Winding Order remains important as our next test needs to start off with the origin “outside” this Triangle.
There’s no need to dwell on the next two tests. They’re exactly the same, it’s just that the Triangles change. And again, if the origin is found to be outside then we have to be very careful of the Winding Order of the new Triangle that will be used for our next test. First here’s triangle ACD:
const Math::Vector& ac_x_ad = Math::cross_product(ac, ad);
if (Math::dot_product(ac_x_ad, ao) > 0) {
m_v[2] = m_v[3];
--m_size;
return std::make_tuple(false, ac_x_ad);
}
And lastly Triangle ADB:
const Math::Vector& ad_x_ab = Math::cross_product(ad, ab);
if (Math::dot_product(ad_x_ab, ao) > 0) {
m_v[1] = m_v[0];
m_v[0] = m_v[2];
m_v[2] = m_v[3];
--m_size;
return std::make_tuple(false, ad_x_ab);
}
And all of that work brings us to the final, glorious step in the GJK. If the origin is not outside of the 4 Triangles, then it can only be in one place, inside the Tetrahedron. This is the success case, proving that the Minkowski Difference contains the origin and our two models are intersecting.
return std::make_tuple(true, Math::Vector()); }
Let’s revel in that for a moment. That simple “true” in the returned tuple means that the collision exists. It took us 3 posts to get here, but we’ve finally come to the end of GJK.
So where do we go from here? What’s the next step? Well you’ll notice that we’ve found that the objects collide, but we don’t know WHERE they collide. If you just want a simple game where you only have to figure out if a laser hit something, then this is all you need. But in most cases we want the thing that was hit to move realistically from the impact. This requires that we know where it was hit. This is a job for our next topic, the EPA. Stay tuned.
| << GJK Part 2 | Contents |