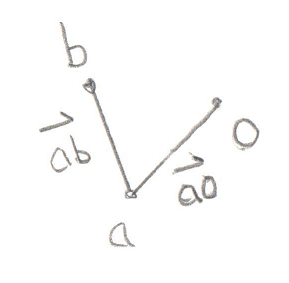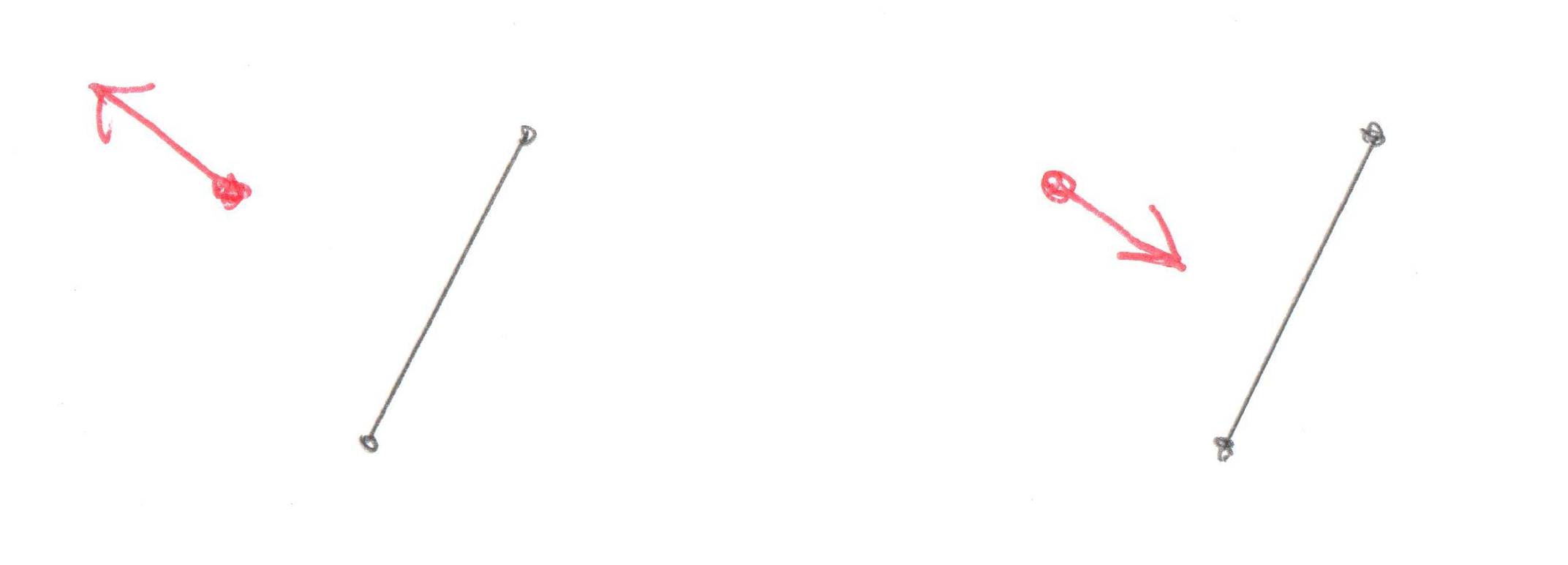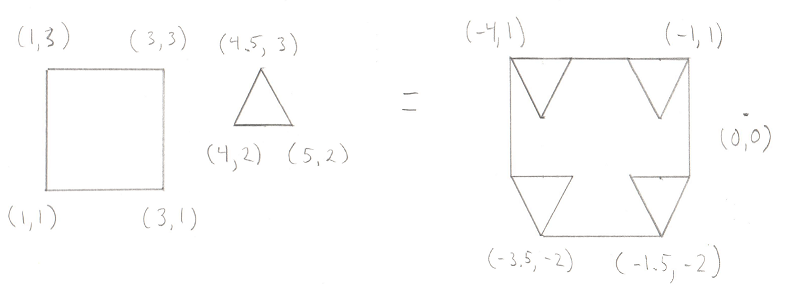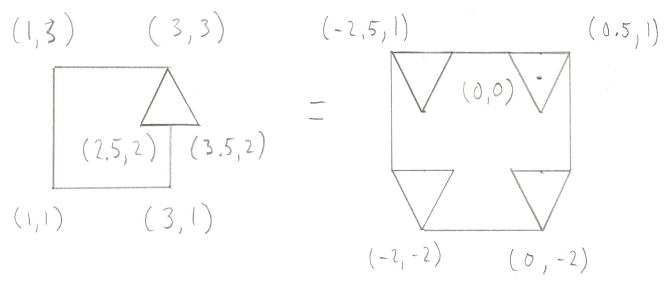Welcome to the final post on implementing the GJK. In the first post, we looked at some of the basics and described the algorithm in general terms. In the second post we looked at how the GJK is set up in the Dubious Engine. In this post we’re going to dig down into the lowest layer, where we build and maintain the Minkowski Simplex.

Let me set the stage from our last post. We were in a loop, trying to find a new Support Point and Support Vector. If a suitable candidate was found, the loop would end like this (not really, but close, the real code is here)

    simplex.push_back( support_point);
    bool collision_found = simplex.build();
    if (collision_found) {
        return true;
    }

So we’re going to be looking at the Minkowski_simplex in detail. Internally it basically holds 4 points (the code is a little bit more complicated for efficiency’s sake). Why 4 points? Remember that in 3D a simplex is a tetrahedron, which is a shape made of 4 points. Not all 4 points are in use at all times. The algorithm starts with a simple Line (ie 2 points). When a new Support Point is added, the simplex becomes a Triangle. Then another new Support Point turns it into a Tetrahedron. If that is not found to contain the origin, then a point is dropped and the simplex becomes a Triangle again. Let’s take a look at how it works.

The Minkowski_simplex::push_back function is trivial. If it were implemented with an actual std::vector it would literally be a call to std::vector::push_back. But what’s up with the build function?

std::tuple<bool, Math::Vector>
Minkowski_simplex::build()
{
    switch (m_size) {
    case 2:
        return build_2();
    case 3:
        return build_3();
    case 4:
        return build_4();
    default:
        throw std::runtime_error("Received simplex of incorrect size");
    }
}

As you can see, there are only three valid point counts, corresponding to the Line, Triangle, and Tetrahedron.

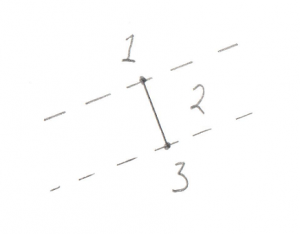
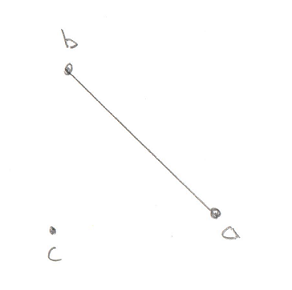
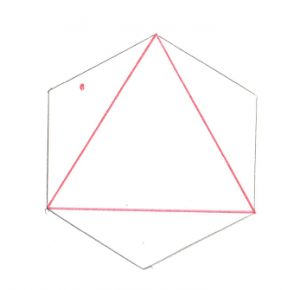
Test 1: Line

Given a simple Line of only two Points, this image shows the 3 possible areas where the origin could be:

1. Past the end of the Line
2. Between the two ends of the Line
3. Past the other end of the Line

Hopefully that’s not too confusing. It turns out that there are actually less real possibilities. Recall in the previous post I devoted a lot of time to the dot_product test between the Support Point and Support Vector. I said it was “critically important.” The reason it’s so critical is that it lets us disregard areas 1 and 3 in the above image. This is because areas 1 and 3 correspond to a situation where the Support Point is out past the end of the Support Vector. And our dot_product test is done to look for exactly this situation, because if the Support Point is out past the end of the Support Vector then there’s no way the resulting simplex can contain the origin. To say it another way, the dot_product test has already filtered out areas 1 and 3, so we don’t even need to look for them. This makes the search for the origin in relation to this line very easy, the origin is either on one side or the other.

Let’s have a look at the code.

std::tuple<bool, Math::Vector>
Minkowski_simplex::build_2()
{
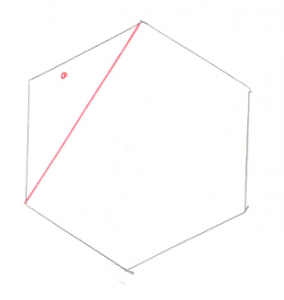
    const Math::Vector& a = m_v[1].v();
    const Math::Vector& b = m_v[0].v();
    const Math::Vector  origin;

    const Math::Vector& ab        = b - a;
    const Math::Vector& ao        = origin - a;

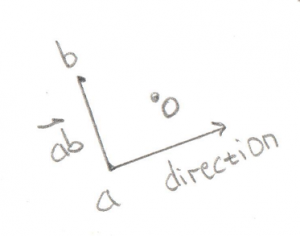
You’ll notice in all this code I try to name things consistently. Points in the simplex are a, b, c, and d, and the origin is o. A Vector pointing from a to b (counter-intuitively calculated by b-a) is called ab.

For this next bit I’m changing the real code by inserting a tmp Vector to make it a bit clearer

    Math::Vector        tmp = Math::cross_product(ab, ao);
    Math::Vector        direction = Math::cross_product( tmp, ab);

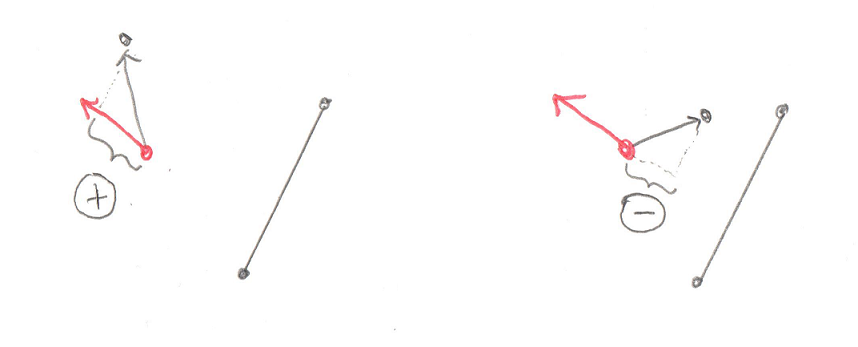
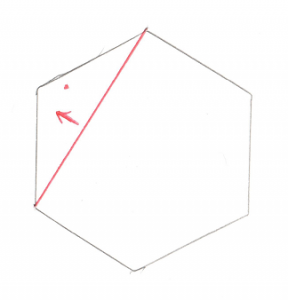
Okay, this is the important part of this test. Let’s look at what’s going on with these two Cross Products. What we’re trying to find is the direction of the origin. Let’s use this as an example, in this image we have Vectors ab and ao:

You’ll recall that a Cross Product of any two Vectors is a third Vector that is perpendicular to both of them. In this case the two Vectors both lie on the plane of your monitor, so the Cross Product of ab and ao, stored in tmp, is a new Vector that points directly out of your monitor and at you. Grab a pencil and stick the eraser on point a and point the tip at you, that’s the Vector tmp. The next part of the code takes the Cross Product of tmp and ab. That would be a new Vector that’s perpendicular to ab and points in the direction of the origin.

Pretty cool, huh? By using two Cross Products we’ve found the direction Vector we’re looking for. That will become the new Support Vector for the next phase of the GJK.

But before we move ahead, there’s an edge case to worry about (there’s always an edge case).

    if (direction == Math::Vector()) {
        if (Math::equals(fabs(ao.y()), 0) && 
            Math::equals(fabs(ao.x()), 0)) {
            direction = Math::Vector(0, 1, 0);
        }
        else {
            direction = Math::Vector(ao.y(), -ao.x(), 0);
        }
    }
    return std::make_tuple(false, direction);
}

If the origin happens to fall exactly on the Vector ab, then the Cross Product will fail and we’ll be left with an empty direction Vector. In this case we can try to create a perpendicular Vector manually.

So that’s the code for the Line test. Not too bad I hope. The following tests are basically the same idea, but with more possible locations to look for the origin, and a few quirks to deal with.

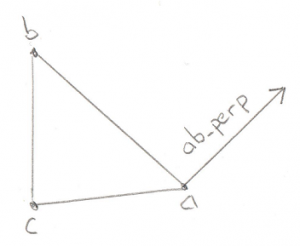
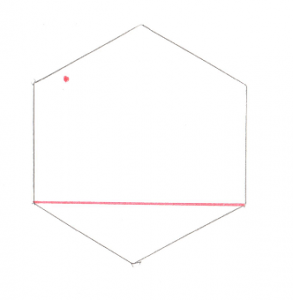
Test 2: Triangle

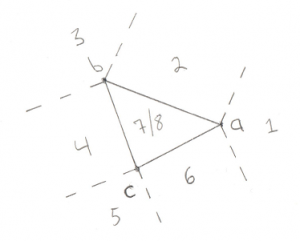
This one is a bit more complex, but it still breaks down into distinct places where the origin can be:

1. Past Point A (not possible)
2. Outside line AB
3. Past Point B (not possible)
4. Outside line BC (not possible)
5. Past Point C (not possible)
6. Outside line CA
7. Above the triangle
8. Below the triangle

We can eliminate cases 1, 3, and 5 due to the same optimization discussed for the Line test, if the origin was past the lines then we would give up before entering this test. We can also eliminate the outside of Vector bc. This is a bit of a surprise. This is because Vector bc turns out to be the Line we tested previously. In order to get to this stage we already know that the origin is on one side of Vector bc, so there’s no need to test the other side. What’s left is 2 Line tests (cases 2 and 6) and 2 Triangle tests (cases 7 and 8).

Let’s look at some code:

std::tuple<bool, Math::Vector>
Minkowski_simplex::build_3()
{
    const Math::Vector& a = m_v[2].v();
    const Math::Vector& b = m_v[1].v();
    const Math::Vector& c = m_v[0].v();
    const Math::Vector  origin;

    const Math::Vector& ab      = b - a;
    const Math::Vector& ac      = c - a;
    const Math::Vector& ao      = origin - a;
    const Math::Vector& ab_x_ac = Math::cross_product(ab, ac);

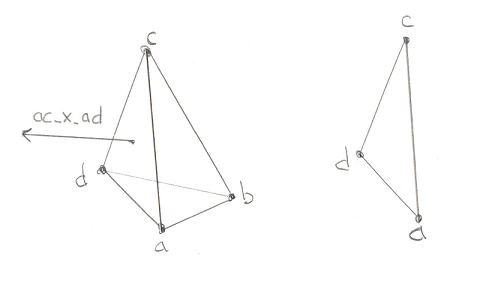
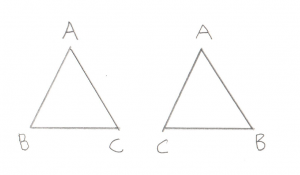
I discussed the naming of a, b, and c previously. It’s important to note that b and c are the same Points used in the above Line test. This is how we can exclude the test on the outside of bc. Vectors ab, ac, and ao are simply created by subtracting the points, same as last time. Vector ab_x_ac (pronounced “ab cross ac”) is the Triangle Normal, ie a Vector pointing perpendicular to the outside of the Triangle. Recall the discussion of the Winding Order, it’s very important that this Triangle is ABC and not ACB. You will see the code moving points around to make sure the winding remains consistent.

So what’s the plan of attack? For the lines tests (cases 2 and 6) we want to find a Vector that points away from an edge, and then test if the origin overlaps with that Vector. Let’s start with the ab edge:

    const Math::Vector& ab_perp = Math::cross_product(ab, ab_x_ac);
    if (Math::dot_product(ao, ab_perp) > 0) {
        m_v[0] = m_v[1];
        m_v[1] = m_v[2];
        --m_size;
        return std::make_tuple(false, ab_perp);
    }

The Vector ab_perp is a Vector perpendicular to edge ab.

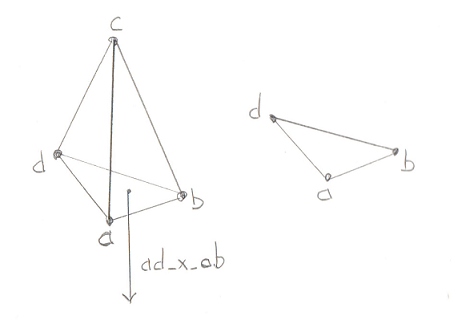
Again we can use the Cross Product to find a Vector perpendicular to any two Vectors, in this case edge ab and the Triangle Normal. We can take the dot product of this new Vector and the ao Vector to find out if ao is on the outside of the Triangle along ab_perp. If it is then we throw away point c and reduce our Minkowski Simplex to a simple Line, and return a new Support Vector to search in.

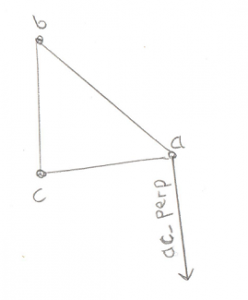
If that test fails then we want to do the exact same test, but this time along edge ac:

    const Math::Vector& ac_perp = Math::cross_product(ab_x_ac, ac);
    if (Math::dot_product(ao, ac_perp) > 0) {
        m_v[1] = m_v[2];
        --m_size;
        return std::make_tuple(false, ac_perp);
    }

If this test passes then the origin is outside of the triangle on the ac side.

This means we have to throw away point b.

If none of these tests find the origin then we can conclude that it’s not outside of any of the edges, so it must be inside the Triangle. So now it’s just a question of whether the origin is above the triangle, or below it.

    float side_check = Math::dot_product(ab_x_ac, ao);
    if (side_check > 0) {
        return std::make_tuple(false, ab_x_ac);
    }

The check to see if it’s above the triangle is trivial, just use the Dot Product to see if Vector ao is along the Triangle Normal. If it is then we retain our entire Triangle and return the new Support Vector.

Finally if it’s not above our Triangle, it must be below it (okay fine, or precisely on it but that edge case doesn’t need to be handled differently)

    std::swap(m_v[0], m_v[1]);
    return std::make_tuple(false, ab_x_ac * -1);
}

Wait wait, what’s going on with the call to std::swap? Remember I said that the Winding Order is important? For our Tetrahedron test we need to know which side of the Triangle the origin is on. I set it up so that it’s always on the “outside.” But in this case, the origin is “inside” the Triangle. So I fix this by simply flipping two points on the Triangle, thereby reversing the Winding Order and making the old “inside” the new “outside.” Cool trick, huh?

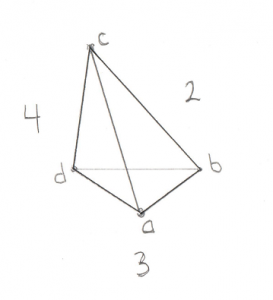
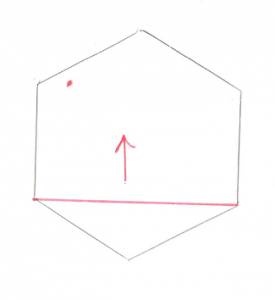
Test 3: Tetrahedron

Hoo boy, the Tetrahedron! If you’re comfortable with the triangle case then this one isn’t a stretch of the imagination. It is, however, a stretch of my drawing abilities:

For this image assume Point a is closest to you. Here’s the places where the origin could be:

1. Past any of the 4 points (not possible)
2. Outside triangle ABC
3. Outside triangle ADB
4. Outside triangle ACD
5. Outside triangle BDC (not possible)
6. Inside the Tetrahedron

I compressed the 4 end point checks into case 1. As before, they’re not possible in our situation due to the Dot Product test that I’ve been harping on about. And just like for the Triangle case it wasn’t possible to be outside of the Line we started with, for the Tetrahedron it’s not possible to be outside of the Triangle we started with (case 5).

Then there are 3 remaining triangle tests. If it turns out that the origin is outside of one of these Triangles then we drop the Point at the opposite side and are left with just a Triangle. Then we define the Support Vector to be in the direction from this Triangle to the origin. We grab a new Point and are left with a new Tetrahedron and the tests begin again.

Let’s bring on the code:

std::tuple<bool, Math::Vector>
Minkowski_simplex::build_4()
{
    const Math::Vector& a = m_v[3].v();
    const Math::Vector& b = m_v[2].v();
    const Math::Vector& c = m_v[1].v();
    const Math::Vector& d = m_v[0].v();
    const Math::Vector  origin;

    const Math::Vector& ab = b - a;
    const Math::Vector& ac = c - a;
    const Math::Vector& ad = d - a;
    const Math::Vector& ao = origin - a;

This bit should look very familiar by now. Let’s be very specific about the Winding Order. You’ll remember from the Triangle test above that we left with the Support Vector on the “outside” of the triangle. Since the new point would have been pushed back to the last position in the array, this means that points b, c, and d define the Triangle we were looking at before. This also means that a is “outside” the Triangle, and that from a‘s perspective, b, c, and d are wound counter-clockwise.

Next we set up the usual edge Vectors, ab, ac, ad, and the Vector to the origin, ao. We don’t bother defining the other edges (bc, bd, or cd) because we already know the origin can’t be outside of that Triangle (case 5 above) so there’s no need.

Let’s have a look at the test outside of Triangle ABC (case 2):

    const Math::Vector& ab_x_ac = Math::cross_product(ab, ac);
    if (Math::dot_product(ab_x_ac, ao) > 0) {
        m_v[0] = m_v[1];
        m_v[1] = m_v[2];
        m_v[2] = m_v[3];
        --m_size;
        return std::make_tuple(false, ab_x_ac);
    }

The Vector ab_x_ac (pronounced “ab cross ac”) is the Normal to Triangle ABC. By checking the Dot Product of that Normal with the Vector to the origin we can see if the origin is outside Triangle ABC. If it is then Triangle ABC becomes our new starting Triangle and ab_x_ac becomes out new Support Vector. This means we drop point d as we know the origin is not on that side of the Tetrahedron. Winding Order remains important as our next test needs to start off with the origin “outside” this Triangle.

There’s no need to dwell on the next two tests. They’re exactly the same, it’s just that the Triangles change. And again, if the origin is found to be outside then we have to be very careful of the Winding Order of the new Triangle that will be used for our next test. First here’s triangle ACD:

    const Math::Vector& ac_x_ad = Math::cross_product(ac, ad);
    if (Math::dot_product(ac_x_ad, ao) > 0) {
        m_v[2] = m_v[3];
        --m_size;
        return std::make_tuple(false, ac_x_ad);
    }

And lastly Triangle ADB:

    const Math::Vector& ad_x_ab = Math::cross_product(ad, ab);
    if (Math::dot_product(ad_x_ab, ao) > 0) {
        m_v[1] = m_v[0];
        m_v[0] = m_v[2];
        m_v[2] = m_v[3];
        --m_size;
        return std::make_tuple(false, ad_x_ab);
    }

And all of that work brings us to the final, glorious step in the GJK. If the origin is not outside of the 4 Triangles, then it can only be in one place, inside the Tetrahedron. This is the success case, proving that the Minkowski Difference contains the origin and our two models are intersecting.

    return std::make_tuple(true, Math::Vector());
}

Let’s revel in that for a moment. That simple “true” in the returned tuple means that the collision exists. It took us 3 posts to get here, but we’ve finally come to the end of GJK.

So where do we go from here? What’s the next step? Well you’ll notice that we’ve found that the objects collide, but we don’t know WHERE they collide. If you just want a simple game where you only have to figure out if a laser hit something, then this is all you need. But in most cases we want the thing that was hit to move realistically from the impact. This requires that we know where it was hit. This is a job for our next topic, the EPA. Stay tuned.

<< GJK Part 2

Contents

In the previous post we looked at how Collision Detection using GJK is supposed to work. In this post, let’s look at how it’s implemented in the Dubious Engine. We’ll start by taking a look at the objects that we’ll be using.

• Physics_model – This is the representation of a model for the purpose of collision detection. It is made up of a std::vector (ie a container) of Local_vectors. I think it’s interesting to notice that we don’t have to keep Edge information, that is we don’t care how Vectors are connected to each other. We just need all of the Vectors that make up the model. Now maybe philosophically these should be Local_points, but there will be so many dot products and cross products that it’s better to just keep them as Vectors. Notice they are stored in local space. This means that when you rotate a model, the points are not actually updated. Instead we keep track of the rotation with a Coordinate_space.
• Coordinate_space – We spoke about these in depth before. Now’s our chance to actually use them. The Coordinate_space defines the position and rotation that applies to all of the Local_vectors in the Physics_model. They are stored next to the Physics_model in a Physics_object (which isn’t really used in collision detection).
• Minkowski_vector – This is just a Vector and some extra data that we won’t be using in the GJK. When I wrote the GJK for the first time, I didn’t have this, so you can just read it as Vector when you see it. Later, when we look at the next step in Collision Detection, the (spoiler alert) EPA, we will see why we need this.
• Minkowski_simplex – This is the big one, it’s where the magic happens. A simplex (as I understand it) is the simplest convex shape that can be created in the number of dimensions you are working with. In 1D it’s a line, in 2D it’s a triangle, in 3D it’s a tetrahedron. If you’ll recall in the previous post I showed how GJK works in 2D using a triangle. In that case the triangle was our simplex. In this post we’ll go full 3D, so we’re talking tetrahedrons. It’s called a Minkowski Simplex because it’s created by using some of the points from a “Minkowski Difference” (also covered in the last post).
• Collision_solver – This is the part that pulls everything together and directs the action. It does more then just the GJK, so we won’t be looking at the whole thing, just the part that’s of interest for now. We’ll come back to it when we go over the EPA.

From the Top

Okay, here we go. We’ll start from the top of our Collision_solver at the public function

bool
Collision_solver::intersection(const Physics_object& a, 
                               const Physics_object& b,
                               std::vector<Contact_manifold::Contact>& 
                               contacts) const

Objects a and b are the two things we want to test for a collision. The GJK doesn’t actually tell us where something collides, only that it does collide.  So for now we won’t concern ourselves with the contacts. Objects a and b are trees of Convex Polyhedra. Remember in the last post I said that complex shapes (like a star) are made up of a bunch of Convex Polyhedra? Well the Physics_object is what contains all of those Polyhedra.

Before we go through how the Physics_objects are compared, let’s look at a very important utility function:

Math::Local_vector
support(const Physics_model& model, const Math::Local_vector& direction)
{
    Math::Local_vector result;
    float              max_dot = std::numeric_limits<float>::lowest();
    for (const auto& v : model.vectors()) {
        float dot = Math::dot_product(v, direction);
        if (dot > max_dot) {
            max_dot = dot;
            result  = v;
        }
    }
    return result;
}

Recall that in the GJK we often want to find the point furthest along a “Support Vector.” Not surprisingly, this point is called the “Support Point.” A brute force method for doing this would be to find the dot product of every point in the model with a Support Vector. Recall from our that the dot product of two Vectors returns a scalar that is related to how much the two Vectors overlap. If we find the Vector in our Physics_model that overlaps the most with our Support Vector, we have found our Support Point.

It’s good to pay attention to which coordinate space we are in for this function. Recall that the points in a Physics_model are in local space. Similarly the direction argument is also a Local_vector. This means it’s reasonable to find the dot_product between the direction and all of the Loval_vectors that make up the Phyics_model. This wouldn’t be possible if direction was in the global space.

Notice that I said this is a brute force method for finding a Support Point. There are ways to do a better job of this, but I never looked into them. I’ve seen mention of a “Hill Climbing” algorithm that might be worth looking up if you’re interested.

Now that we know how to find a Support Point, let’s continue with how to search the Physics_models for collisions. The Dubious Engine code has a few uninteresting layers where we just traverse the various trees until we get to a place where we actually start comparing Physics_models. Let’s take a look at the important parts of this code.

bool
intersection_recurse_b(const Physics_model& a, 
                       const Math::Coordinate_space& ca,
                       const Physics_model& b, 
                       const Math::Coordinate_space& cb,
                       std::vector<Contact_manifold::Contact>& contacts)
{
    bool              ret_val = false;
    Minkowski_simplex simplex;
    if (model_intersection(a, ca, b, cb, simplex)) {
        ret_val = true;
    }
    for (const auto& kid : b.kids()) {
        if (intersection_recurse_b(a, ca, *kid, cb, contacts)) {
            ret_val = true;
        }
    }

    return ret_val;
}

At this point we’ve dropped inside the Physics_objects to get the Physics_models and their Coordinate_spaces. We create a new simplex and then check the models to see if there’s an intersection. Lastly, we compare Physics_model a with Physics_model b and all its children. Clearly that model_intersection function is a big one as it determines whether or not the models have intersected. We’ll spend the rest of this post looking into this function (full listing here)

bool
model_intersection(const Physics_model& a, 
                   const Math::Coordinate_space& ca, 
                   const Physics_model& b,
                   const Math::Coordinate_space& cb, 
                   Minkowski_simplex& simplex)
{
    Math::Vector direction(1, 0, 0);
    Math::Vector support_a =
        ca.transform(support(a, ca.transform(direction))) + 
        (Math::to_vector(ca.position()));
    Math::Vector support_b =
        cb.transform(support(b, cb.transform(direction * -1))) + 
        (Math::to_vector(cb.position()));
    Math::Vector support_point = support_a - support_b;

This first part is all about setting up the starting point. We randomly pick a Support Vector of (1,0,0) to start. Next we find the Support Point in model a and the Support Point in model b. For model b we’re actually using a Support Vector in the opposite direction. This is because a Minkowski Difference is made from subtracting b from a.

Notice all the calls to transform. What’s happening is that the Support Vector, direction, is in Global Space (ie it’s a Vector, not a Local_vector). But as I mentioned previously, the support function needs this vector to be in Local Space, so we use the Coordinate_space to transform the Vector into a Local_vector. From there we can call support, which returns a Local_vector, which we then need to transform back into Global Space, again with the help of the Coordinate_space object. This should give you an appreciation for using types to your advantage. Once we have the Support Points on both Physics_models we want to find the Support Point on the Minkowski Difference. Remember that the Minkowski Difference is made from taking a point on model b and subtracting it from a point on model a. And since both of our support points are in a global Coordinate_space, we can simply subtract them to get a new support_point on the Minkowski Difference.

However there is an edge case we need to worry about:

    if (support_point == Math::Vector()) {
        direction = Math::Vector(0, 1, 0);
        support_a =
            ca.transform(support(a, ca.transform(direction))) + 
            (Math::to_vector(ca.position()));
        support_b = 
            cb.transform(support(b, cb.transform(direction * -1))) +
            (Math::to_vector(cb.position()));
        support_point = support_a - support_b;
    }
    simplex   = Minkowski_simplex(Minkowski_vector(support_point, 
                                                   support_a, 
                                                   support_b));
    direction = support_point * -1;

The support_point we found is going to be used to start our Minkowski_simplex, and we would like for the next Support Vector, direction, to simply be a Vector in the opposite direction of this point. However if our current point just happens to fall on the origin, then the new Support Vector will be empty and the entire function falls apart. So if that happens we basically start over but use the vector (0,1,0) as our starting Support Vector.

In the end we have a support_point and a new Support Vector. You can ignore the Minkowski_vector class for now (just pretend it’s only the support_point). Next we create a new Minkowski_simplex.

The next bit is a loop that really should continue until a collision is either found or not found. However there can be edge cases where rounding errors cause us to bounce back and forth between the two states, so we’re just going to try the loop a fixed number of times and if we don’t converge on a solution, assume the objects are not touching. In practice this isn’t the end of the world because the objects will probably just intersect even more during the next update and we’ll catch them then.

    int i = 0;
    for (i = 0; i < 20; ++i) {
        support_a =
            ca.transform(support(a, ca.transform(direction))) + 
            (Math::to_vector(ca.position()));
        support_b = 
            cb.transform(support(b, cb.transform(direction * -1))) +
            (Math::to_vector(cb.position()));
        support_point = support_a - support_b;

This bit should look pretty familiar by now. direction is the Support Vector and we’re just looking for the Support Points along it on both objects. We already did this to start up the Minkowski_simplex above.

This next bit is critically important. If you need to take a break and get some coffee, now is a good time. Once you’re feeling refreshed, have a look at this:

        if (Math::dot_product(support_point, direction) <= 0) { 
          return false; 
        } 

So what’s going on here? We know that the Support Vector, direction, points away from the existing points in the Minkowski_simplex towards the origin. How do we know this? Well the whole point of the GJK is to see if the Minkowski_simplex contains the origin. So if we already have a bunch of points on one side of the origin, the only way to contain the origin is to look for a point on the other side of the origin.

This image should make it clearer. In these drawings the dark line represents the current part of the Minkowski_simplex. The red dot is the origin, and the red arrow is the proposed Support Vector.

In the left side drawing the Support Vector is pointing from the simplex through the origin and it’s obvious that if there’s a point in that direction the resulting triangle might contain the origin. In the drawing on the right it doesn’t matter which point you find in the direction of the Support Vector, there’s no way it could ever contain the origin.

So back to the code, it’s clear the Support Vector must be pointing away from the existing points and through the origin. We want to test that Support Vector against the new support_point. The dot product of two vectors will tell you if they overlap.

In the left side image the dot product between the support Vector and the Vector to the new support_point is positive (see the helpful + sign in the circle?). This means it’s possible for the new support_point to create a simplex that contains the origin. In the image on the right the dot product is negative (that’s a – sign in the circle) and there’s no way the new simplex could contain the origin.

Knowing all that, let’s look at the code again and it should be clear

        if (Math::dot_product(support_point, direction) <= 0) { 
          return false; 
        } 

If the dot product between the support_point and the Support Vector, direction, is negative then there’s no way the simplex could contain the origin. This means there’s no way the objects could be colliding, so we return false.

That’s a lot of information to take in about one little dot product. Another important bit is that we’re checking for less then or equal, not just less then. Why is this? Is the dot product is 0 it means that the two objects are just barely touching. You could consider this a collision, but I found that it breaks the next step, the EPA. So in the Dubious Engine, objects that just touch are not considered colliding.

So continuing on, if it turns out that the dot_product returns positive, then the new Support Point is on the other side of the origin from the existing points in the Minkowski_simplex. That doesn’t necessarily mean the Minkowski_simplex contains the origin, only that it might. So we’ll want to add this new Support Point to our simplex and test it out.

        simplex.push_back(Minkowski_vector(support_point, 
                                           support_a, 
                                           support_b)); 
        bool collision_found; 
        std::tie(collision_found, direction) = simplex.build(); 
        if (collision_found) { 
          return true; 
        } 
    }

    return false;
}

And this brings us to the end of this function. However there is a lot more to explore. Inside that call to simplex.build() is where the simplex is tested to see if it contains the origin. If it does not then the simplex changes shape and returns a new Support Vector, direction, to search for the next support_point.

That’s a lot of code to stare at in one post. And there’s a lot more code still to come. So I’m going to wrap this up. The next post should be the last one that describes the GJK. From there I’ll introduce this EPA I’ve mentioned a couple of times. That one is what tells us where the collision takes place. Something to look forward to.

<< GJK Part 1

Contents

GJK Part 3 >>

Hopefully by now you’ve got a foundation of the Math required for a Physics Engine and you’ve understood the Physics of motion, both linear and angular. With just that knowledge you’d be able to create a simple game where objects fly around in a realistic manner. That’s all well and good, but what fun is a game if things can’t smash into each other and explode? With this post we’ll start to talk about how to detect whether or not two objects are smashing into each other. This will be the first step into the really fun parts of writing a Physics Engine.

So where do we start? The first thing we have to do is figure out a way to detect if two objects are colliding. This is called, not surprisingly, “Collision Detection.” It’s actually not hard to imagine an algorithm that will figure this out for us. The trick is finding an algorithm that can do it 60 times a second.

It’s All Trianlges

Maybe before we even talk about Collision Detection it is important to define what’s colliding. An object in a 3D Game is represented as a whole bunch of Points that define Triangles in space. Why Triangles? Well they’re the simplest 3D object you can represent. And you can combine them together to form a shell for anything. There’s one problem however, which is that Triangles don’t have an “inside” and an “outside.” You can create a cube made up of a whole bunch of Triangles (12 of them actually) and by looking at the cube you know what’s inside, but if you pick any triangle at random, you’ll have no idea which side is inside. We could solve this by storing a Vector perpendicular to the Triangle pointing out (this is called the Normal). But that would mean we’d have to store an extra vector, which is 33% more data then just storing 3 points. That’s a heck of a lot of bloat.

Instead of paying that cost people noticed that the order of the points on a Triangle can be used. Given three points: A, B, and C, we can order them in two ways: ABC or ACB. Most systems work such that if you’re outside the Triangle looking in then the points will be listed counter-clockwise. This convention tells us which direction is “outside” without needing to store an extra Vector.

If we called this triangle ABC, then for the left triangle we are outside looking in. For the right triangle we are inside looking out.

Okay, so let’s imagine we have two objects, both made up of a whole bunch of points and triangles, written such that we know which direction is the inside. Collision detection between these two objects is actually trivial. Let’s say you have a function that checks whether or not a point is inside another object:

bool point_inside( const Point& p, const Model& object );

This function could just compare the point against every single triangle in the object to see if it’s inside it. In this case, Collision Detection would just be easy, just take every point in object A and see if it’s inside object B. If any points are inside then the objects are colliding. This doesn’t get all cases though as an edge can be inside an object even if both its endpoints are outside. So you would also write a check to see if an edge is inside and compare all edges.

bool edge_inside( const Point& p1, const Point& p2, const Model& object );

Unfortunately, all of these checks would make our test very slow. We’re talking about a lot of checks. Still it’s nice to know that an easy solution exists, makes the whole challenge seem less daunting.

A better solution would be able to find the same thing, but do it in far fewer checks. There are actually a number of solutions out there. We’ll be talking about GJK, named after its creators: Gilbert, Johnson, and Keerthi. But before we dive in it’s important to note that all of the solutions I’ve run across have a restriction that they only work on “Convex Polyhedra.” What is this? It’s an object where if you were to draw a line between any pair of points, the line would either be on the skin of the object or inside the object. More intuitively, there are no dents on a Convex Polyhedra. The simplest example is a tetrahedron, which is 4 triangles joined up (for you D&D nerds out there, it’s the 4 sided die). Other examples are cubes or spheres. What are not Convex Polyhadra? Things like stars, crescent moons, or pac-man.

Now before you get frustrated and point out that just about all fun objects in a game (cars, space ships, bazookas) are not Convex Ployhedra, notice that all non-Convex Polyhedra can be broken down into Convex Polyhedra. For example a five pointed star can be broken down into a pentagon and five triangles.

A Collision Detection algorithm can simply check if any of the smaller Convex Polyhedra from one object intersects with the smaller Convex Polyhedra from another object. In short, the restriction is not much of a restriction, it just means you have to be a bit careful about how you design your 3D models.

Minkowski Sum

Okay, so now we know that we’re dealing with Convex Polyhedra, and we want to find a more efficient algorithm for checking whether or not they collide, and we know the algorithm we’re gonna use is called GJK. The next bit to learn about is the Minkowski Sum. This incredibly clever trick is surprisingly simple. You just take all of the points from one object and add them to all the points of another object. The result is a sort of mash up of the two objects:

I drew in the edges that would make it clearer, but really maybe I should have connected all the points, or maybe none at all. I’m not really sure what’s “correct” but this should give you an idea. This in itself is not overly helpful. However if you tweak it ever so slightly and instead subtract all of the points of one object from another (sometimes called a “Minkowski Difference”) you get a surprising result. Here’s a picture of a Minkowski Difference of two non-intersecting objects

This time I added in some positions. You can check my math, but the important part is to notice where the origin is in relation to the resulting shape. And here’s one of two intersecting objects:

Notice the origin again. The Minkowski Difference of any two intersecting objects contains the origin. So now we have a surprisingly clever test to see if two objects intersect, we start by creating a Minkowski Difference of the two objects and test to see if that result contains the origin.

Making it Efficient

But wait, is that any more efficient then our simple comparison that we started with? We still end up operating on every pair of points on the two objects, which is still a lot of points. The operations (subtraction) are quicker then checking if a point or line is inside a triangle, but it’s still a lot of operations. So yeah, it’s still not a great solution.

However it’s easy to improve on by noticing that you don’t actually need the entire Minkowski Difference to check to see if it contains the origin. If any tetrahedron (or triangle in 2D) within the Minkowski Difference contains the origin, then the entire Minkowski Difference contains the origin. We also know that given the choice to look for really small tetrahedrons or really big tetrahedrons, it would make more sense to look for the really big ones, as they contain much more volume in general, and as such have a higher chance of containing the origin.

 

Plan of Attack

Okay, now we have enough information to understand the algorithm. The goal is to see if we can create a tetrahedron (4 sided, pyramid like shape) from the Minkowski Difference that contains the origin. If we can then the objects overlap, if not, they don’t. Unfortunately, drawing this algorithm in 3D is tough, so I’m going to drop down to 2D. In this case, we’re not looking for a tetrahedron that contains the origin, we’re looking for a triangle. Much simpler to draw triangles.

Let’s set the stage with a simple shape that contains the origin. We’re going to pick any arbitrary line between any two points on this shape as our starting point. This line is known as the “Support Vector” in the GJK.

The red dot to the upper left is the origin, and the red line just connects any two points. From here we can do some simple math and figure out where the origin is in relation to our line. From looking at the picture it’s pretty obvious

The origin is above the line. That arrow becomes our Support Vector and the next step is to find the point that is furthest along that Support Vector. Pretty easy to see that the top most point is the one we’re looking for. If you add that point to the existing line you get a Triangle

Now that’s all well and good, but there’s a problem, the origin isn’t inside that triangle. We can do some math to prove it and find out that the origin is to the left of the leftmost line. This means that the right most point is no longer of interest to us, so we can throw it away and we’ll find ourselves back to the case of a single line

And again, we want to figure out where the origin is in relation to the single line. Pretty obvious that it’s on the left side.

And just like before, that arrow becomes our Support Vector. And we want to find the point furthest along in that direction. And if we add that point to our existing line, we create a new triangle.

This new triangle contains the origin. Huzzah! Since a triangle inside the Minkowski Difference contains the origin, the original two shapes are intersecting, we have a collision.

If you are a bit unclear, why not have a look at another article explaining the same thing. I have to give the author credit for using sticks and clay to create a 3D representation of the GJK. Well done!

In the next post, we’ll take a look at the specifics of the algorithm and the code.

<< Angular Motion

Contents

GJK Part 2 >>