In the previous post we looked at how Collision Detection using GJK is supposed to work. In this post, let’s look at how it’s implemented in the Dubious Engine. We’ll start by taking a look at the objects that we’ll be using.
- Physics_model – This is the representation of a model for the purpose of collision detection. It is made up of a
std::vector(ie a container) of Local_vectors. I think it’s interesting to notice that we don’t have to keep Edge information, that is we don’t care how Vectors are connected to each other. We just need all of the Vectors that make up the model. Now maybe philosophically these should be Local_points, but there will be so many dot products and cross products that it’s better to just keep them as Vectors. Notice they are stored in local space. This means that when you rotate a model, the points are not actually updated. Instead we keep track of the rotation with a Coordinate_space. - Coordinate_space – We spoke about these in depth before. Now’s our chance to actually use them. The Coordinate_space defines the position and rotation that applies to all of the Local_vectors in the Physics_model. They are stored next to the Physics_model in a Physics_object (which isn’t really used in collision detection).
- Minkowski_vector – This is just a Vector and some extra data that we won’t be using in the GJK. When I wrote the GJK for the first time, I didn’t have this, so you can just read it as Vector when you see it. Later, when we look at the next step in Collision Detection, the (spoiler alert) EPA, we will see why we need this.
- Minkowski_simplex – This is the big one, it’s where the magic happens. A simplex (as I understand it) is the simplest convex shape that can be created in the number of dimensions you are working with. In 1D it’s a line, in 2D it’s a triangle, in 3D it’s a tetrahedron. If you’ll recall in the previous post I showed how GJK works in 2D using a triangle. In that case the triangle was our simplex. In this post we’ll go full 3D, so we’re talking tetrahedrons. It’s called a Minkowski Simplex because it’s created by using some of the points from a “Minkowski Difference” (also covered in the last post).
- Collision_solver – This is the part that pulls everything together and directs the action. It does more then just the GJK, so we won’t be looking at the whole thing, just the part that’s of interest for now. We’ll come back to it when we go over the EPA.
From the Top
Okay, here we go. We’ll start from the top of our Collision_solver at the public function
bool
Collision_solver::intersection(const Physics_object& a,
const Physics_object& b,
std::vector<Contact_manifold::Contact>&
contacts) const
Objects a and b are the two things we want to test for a collision. The GJK doesn’t actually tell us where something collides, only that it does collide. So for now we won’t concern ourselves with the contacts. Objects a and b are trees of Convex Polyhedra. Remember in the last post I said that complex shapes (like a star) are made up of a bunch of Convex Polyhedra? Well the Physics_object is what contains all of those Polyhedra.
Before we go through how the Physics_objects are compared, let’s look at a very important utility function:
Math::Local_vector
support(const Physics_model& model, const Math::Local_vector& direction)
{
Math::Local_vector result;
float max_dot = std::numeric_limits<float>::lowest();
for (const auto& v : model.vectors()) {
float dot = Math::dot_product(v, direction);
if (dot > max_dot) {
max_dot = dot;
result = v;
}
}
return result;
}
Recall that in the GJK we often want to find the point furthest along a “Support Vector.” Not surprisingly, this point is called the “Support Point.” A brute force method for doing this would be to find the dot product of every point in the model with a Support Vector. Recall from our that the dot product of two Vectors returns a scalar that is related to how much the two Vectors overlap. If we find the Vector in our Physics_model that overlaps the most with our Support Vector, we have found our Support Point.
It’s good to pay attention to which coordinate space we are in for this function. Recall that the points in a Physics_model are in local space. Similarly the direction argument is also a Local_vector. This means it’s reasonable to find the dot_product between the direction and all of the Loval_vectors that make up the Phyics_model. This wouldn’t be possible if direction was in the global space.
Notice that I said this is a brute force method for finding a Support Point. There are ways to do a better job of this, but I never looked into them. I’ve seen mention of a “Hill Climbing” algorithm that might be worth looking up if you’re interested.
Now that we know how to find a Support Point, let’s continue with how to search the Physics_models for collisions. The Dubious Engine code has a few uninteresting layers where we just traverse the various trees until we get to a place where we actually start comparing Physics_models. Let’s take a look at the important parts of this code.
bool
intersection_recurse_b(const Physics_model& a,
const Math::Coordinate_space& ca,
const Physics_model& b,
const Math::Coordinate_space& cb,
std::vector<Contact_manifold::Contact>& contacts)
{
bool ret_val = false;
Minkowski_simplex simplex;
if (model_intersection(a, ca, b, cb, simplex)) {
ret_val = true;
}
for (const auto& kid : b.kids()) {
if (intersection_recurse_b(a, ca, *kid, cb, contacts)) {
ret_val = true;
}
}
return ret_val;
}
At this point we’ve dropped inside the Physics_objects to get the Physics_models and their Coordinate_spaces. We create a new simplex and then check the models to see if there’s an intersection. Lastly, we compare Physics_model a with Physics_model b and all its children. Clearly that model_intersection function is a big one as it determines whether or not the models have intersected. We’ll spend the rest of this post looking into this function (full listing here)
bool
model_intersection(const Physics_model& a,
const Math::Coordinate_space& ca,
const Physics_model& b,
const Math::Coordinate_space& cb,
Minkowski_simplex& simplex)
{
Math::Vector direction(1, 0, 0);
Math::Vector support_a =
ca.transform(support(a, ca.transform(direction))) +
(Math::to_vector(ca.position()));
Math::Vector support_b =
cb.transform(support(b, cb.transform(direction * -1))) +
(Math::to_vector(cb.position()));
Math::Vector support_point = support_a - support_b;
This first part is all about setting up the starting point. We randomly pick a Support Vector of (1,0,0) to start. Next we find the Support Point in model a and the Support Point in model b. For model b we’re actually using a Support Vector in the opposite direction. This is because a Minkowski Difference is made from subtracting b from a.
Notice all the calls to transform. What’s happening is that the Support Vector, direction, is in Global Space (ie it’s a Vector, not a Local_vector). But as I mentioned previously, the support function needs this vector to be in Local Space, so we use the Coordinate_space to transform the Vector into a Local_vector. From there we can call support, which returns a Local_vector, which we then need to transform back into Global Space, again with the help of the Coordinate_space object. This should give you an appreciation for using types to your advantage. Once we have the Support Points on both Physics_models we want to find the Support Point on the Minkowski Difference. Remember that the Minkowski Difference is made from taking a point on model b and subtracting it from a point on model a. And since both of our support points are in a global Coordinate_space, we can simply subtract them to get a new support_point on the Minkowski Difference.
However there is an edge case we need to worry about:
if (support_point == Math::Vector()) {
direction = Math::Vector(0, 1, 0);
support_a =
ca.transform(support(a, ca.transform(direction))) +
(Math::to_vector(ca.position()));
support_b =
cb.transform(support(b, cb.transform(direction * -1))) +
(Math::to_vector(cb.position()));
support_point = support_a - support_b;
}
simplex = Minkowski_simplex(Minkowski_vector(support_point,
support_a,
support_b));
direction = support_point * -1;
The support_point we found is going to be used to start our Minkowski_simplex, and we would like for the next Support Vector, direction, to simply be a Vector in the opposite direction of this point. However if our current point just happens to fall on the origin, then the new Support Vector will be empty and the entire function falls apart. So if that happens we basically start over but use the vector (0,1,0) as our starting Support Vector.
In the end we have a support_point and a new Support Vector. You can ignore the Minkowski_vector class for now (just pretend it’s only the support_point). Next we create a new Minkowski_simplex.
The next bit is a loop that really should continue until a collision is either found or not found. However there can be edge cases where rounding errors cause us to bounce back and forth between the two states, so we’re just going to try the loop a fixed number of times and if we don’t converge on a solution, assume the objects are not touching. In practice this isn’t the end of the world because the objects will probably just intersect even more during the next update and we’ll catch them then.
int i = 0;
for (i = 0; i < 20; ++i) {
support_a =
ca.transform(support(a, ca.transform(direction))) +
(Math::to_vector(ca.position()));
support_b =
cb.transform(support(b, cb.transform(direction * -1))) +
(Math::to_vector(cb.position()));
support_point = support_a - support_b;
This bit should look pretty familiar by now. direction is the Support Vector and we’re just looking for the Support Points along it on both objects. We already did this to start up the Minkowski_simplex above.
This next bit is critically important. If you need to take a break and get some coffee, now is a good time. Once you’re feeling refreshed, have a look at this:
if (Math::dot_product(support_point, direction) <= 0) {
return false;
}
So what’s going on here? We know that the Support Vector, direction, points away from the existing points in the Minkowski_simplex towards the origin. How do we know this? Well the whole point of the GJK is to see if the Minkowski_simplex contains the origin. So if we already have a bunch of points on one side of the origin, the only way to contain the origin is to look for a point on the other side of the origin.
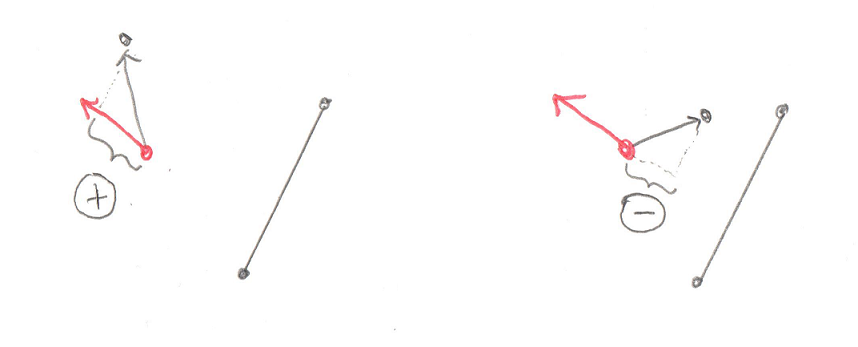
This image should make it clearer. In these drawings the dark line represents the current part of the Minkowski_simplex. The red dot is the origin, and the red arrow is the proposed Support Vector.
In the left side drawing the Support Vector is pointing from the simplex through the origin and it’s obvious that if there’s a point in that direction the resulting triangle might contain the origin. In the drawing on the right it doesn’t matter which point you find in the direction of the Support Vector, there’s no way it could ever contain the origin.
So back to the code, it’s clear the Support Vector must be pointing away from the existing points and through the origin. We want to test that Support Vector against the new support_point. The dot product of two vectors will tell you if they overlap.
In the left side image the dot product between the support Vector and the Vector to the new support_point is positive (see the helpful + sign in the circle?). This means it’s possible for the new support_point to create a simplex that contains the origin. In the image on the right the dot product is negative (that’s a – sign in the circle) and there’s no way the new simplex could contain the origin.
Knowing all that, let’s look at the code again and it should be clear
if (Math::dot_product(support_point, direction) <= 0) {
return false;
}
If the dot product between the support_point and the Support Vector, direction, is negative then there’s no way the simplex could contain the origin. This means there’s no way the objects could be colliding, so we return false.
That’s a lot of information to take in about one little dot product. Another important bit is that we’re checking for less then or equal, not just less then. Why is this? Is the dot product is 0 it means that the two objects are just barely touching. You could consider this a collision, but I found that it breaks the next step, the EPA. So in the Dubious Engine, objects that just touch are not considered colliding.
So continuing on, if it turns out that the dot_product returns positive, then the new Support Point is on the other side of the origin from the existing points in the Minkowski_simplex. That doesn’t necessarily mean the Minkowski_simplex contains the origin, only that it might. So we’ll want to add this new Support Point to our simplex and test it out.
simplex.push_back(Minkowski_vector(support_point,
support_a,
support_b));
bool collision_found;
std::tie(collision_found, direction) = simplex.build();
if (collision_found) {
return true;
}
}
return false;
}
And this brings us to the end of this function. However there is a lot more to explore. Inside that call to simplex.build() is where the simplex is tested to see if it contains the origin. If it does not then the simplex changes shape and returns a new Support Vector, direction, to search for the next support_point.
That’s a lot of code to stare at in one post. And there’s a lot more code still to come. So I’m going to wrap this up. The next post should be the last one that describes the GJK. From there I’ll introduce this EPA I’ve mentioned a couple of times. That one is what tells us where the collision takes place. Something to look forward to.
| << GJK Part 1 | Contents | GJK Part 3 >> |