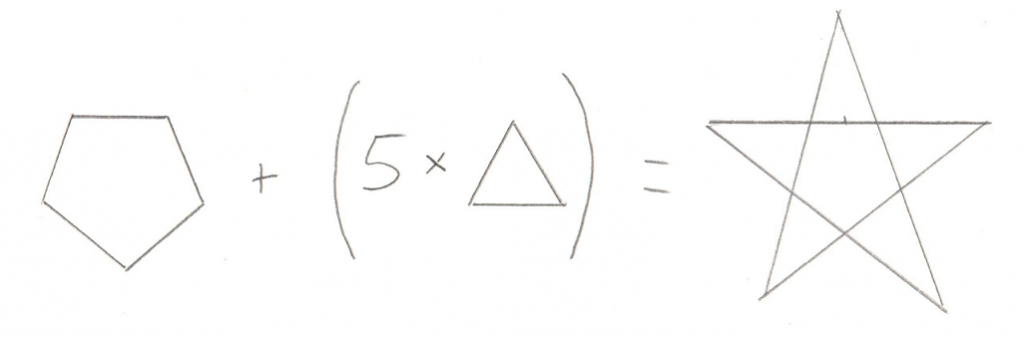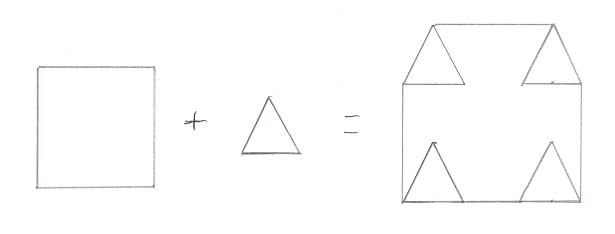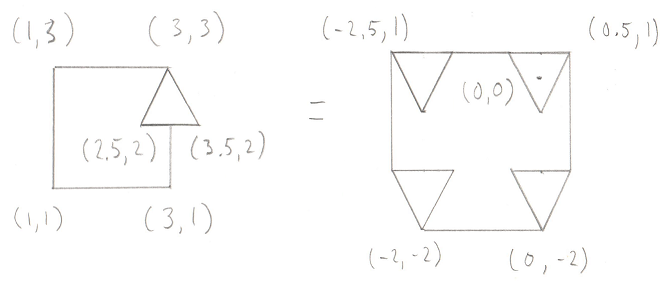Hopefully by now you’ve got a foundation of the Math required for a Physics Engine and you’ve understood the Physics of motion, both linear and angular. With just that knowledge you’d be able to create a simple game where objects fly around in a realistic manner. That’s all well and good, but what fun is a game if things can’t smash into each other and explode? With this post we’ll start to talk about how to detect whether or not two objects are smashing into each other. This will be the first step into the really fun parts of writing a Physics Engine.
So where do we start? The first thing we have to do is figure out a way to detect if two objects are colliding. This is called, not surprisingly, “Collision Detection.” It’s actually not hard to imagine an algorithm that will figure this out for us. The trick is finding an algorithm that can do it 60 times a second.
It’s All Trianlges
Maybe before we even talk about Collision Detection it is important to define what’s colliding. An object in a 3D Game is represented as a whole bunch of Points that define Triangles in space. Why Triangles? Well they’re the simplest 3D object you can represent. And you can combine them together to form a shell for anything. There’s one problem however, which is that Triangles don’t have an “inside” and an “outside.” You can create a cube made up of a whole bunch of Triangles (12 of them actually) and by looking at the cube you know what’s inside, but if you pick any triangle at random, you’ll have no idea which side is inside. We could solve this by storing a Vector perpendicular to the Triangle pointing out (this is called the Normal). But that would mean we’d have to store an extra vector, which is 33% more data then just storing 3 points. That’s a heck of a lot of bloat.
Instead of paying that cost people noticed that the order of the points on a Triangle can be used. Given three points: A, B, and C, we can order them in two ways: ABC or ACB. Most systems work such that if you’re outside the Triangle looking in then the points will be listed counter-clockwise. This convention tells us which direction is “outside” without needing to store an extra Vector.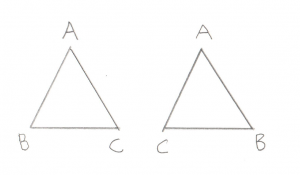
If we called this triangle ABC, then for the left triangle we are outside looking in. For the right triangle we are inside looking out.
Okay, so let’s imagine we have two objects, both made up of a whole bunch of points and triangles, written such that we know which direction is the inside. Collision detection between these two objects is actually trivial. Let’s say you have a function that checks whether or not a point is inside another object:
bool point_inside( const Point& p, const Model& object );
This function could just compare the point against every single triangle in the object to see if it’s inside it. In this case, Collision Detection would just be easy, just take every point in object A and see if it’s inside object B. If any points are inside then the objects are colliding. This doesn’t get all cases though as an edge can be inside an object even if both its endpoints are outside. So you would also write a check to see if an edge is inside and compare all edges.
bool edge_inside( const Point& p1, const Point& p2, const Model& object );
Unfortunately, all of these checks would make our test very slow. We’re talking about a lot of checks. Still it’s nice to know that an easy solution exists, makes the whole challenge seem less daunting.
A better solution would be able to find the same thing, but do it in far fewer checks. There are actually a number of solutions out there. We’ll be talking about GJK, named after its creators: Gilbert, Johnson, and Keerthi. But before we dive in it’s important to note that all of the solutions I’ve run across have a restriction that they only work on “Convex Polyhedra.” What is this? It’s an object where if you were to draw a line between any pair of points, the line would either be on the skin of the object or inside the object. More intuitively, there are no dents on a Convex Polyhedra. The simplest example is a tetrahedron, which is 4 triangles joined up (for you D&D nerds out there, it’s the 4 sided die). Other examples are cubes or spheres. What are not Convex Polyhadra? Things like stars, crescent moons, or pac-man.
Now before you get frustrated and point out that just about all fun objects in a game (cars, space ships, bazookas) are not Convex Ployhedra, notice that all non-Convex Polyhedra can be broken down into Convex Polyhedra. For example a five pointed star can be broken down into a pentagon and five triangles.
A Collision Detection algorithm can simply check if any of the smaller Convex Polyhedra from one object intersects with the smaller Convex Polyhedra from another object. In short, the restriction is not much of a restriction, it just means you have to be a bit careful about how you design your 3D models.
Minkowski Sum
Okay, so now we know that we’re dealing with Convex Polyhedra, and we want to find a more efficient algorithm for checking whether or not they collide, and we know the algorithm we’re gonna use is called GJK. The next bit to learn about is the Minkowski Sum. This incredibly clever trick is surprisingly simple. You just take all of the points from one object and add them to all the points of another object. The result is a sort of mash up of the two objects:
I drew in the edges that would make it clearer, but really maybe I should have connected all the points, or maybe none at all. I’m not really sure what’s “correct” but this should give you an idea. This in itself is not overly helpful. However if you tweak it ever so slightly and instead subtract all of the points of one object from another (sometimes called a “Minkowski Difference”) you get a surprising result. Here’s a picture of a Minkowski Difference of two non-intersecting objects
This time I added in some positions. You can check my math, but the important part is to notice where the origin is in relation to the resulting shape. And here’s one of two intersecting objects:
Notice the origin again. The Minkowski Difference of any two intersecting objects contains the origin. So now we have a surprisingly clever test to see if two objects intersect, we start by creating a Minkowski Difference of the two objects and test to see if that result contains the origin.
Making it Efficient
But wait, is that any more efficient then our simple comparison that we started with? We still end up operating on every pair of points on the two objects, which is still a lot of points. The operations (subtraction) are quicker then checking if a point or line is inside a triangle, but it’s still a lot of operations. So yeah, it’s still not a great solution.
However it’s easy to improve on by noticing that you don’t actually need the entire Minkowski Difference to check to see if it contains the origin. If any tetrahedron (or triangle in 2D) within the Minkowski Difference contains the origin, then the entire Minkowski Difference contains the origin. We also know that given the choice to look for really small tetrahedrons or really big tetrahedrons, it would make more sense to look for the really big ones, as they contain much more volume in general, and as such have a higher chance of containing the origin.
Plan of Attack
Okay, now we have enough information to understand the algorithm. The goal is to see if we can create a tetrahedron (4 sided, pyramid like shape) from the Minkowski Difference that contains the origin. If we can then the objects overlap, if not, they don’t. Unfortunately, drawing this algorithm in 3D is tough, so I’m going to drop down to 2D. In this case, we’re not looking for a tetrahedron that contains the origin, we’re looking for a triangle. Much simpler to draw triangles.
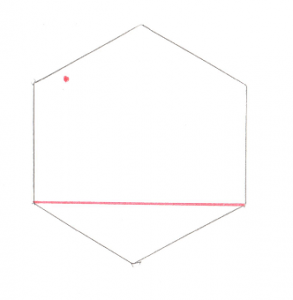
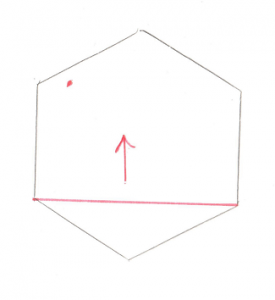
Let’s set the stage with a simple shape that contains the origin. We’re going to pick any arbitrary line between any two points on this shape as our starting point. This line is known as the “Support Vector” in the GJK.
The red dot to the upper left is the origin, and the red line just connects any two points. From here we can do some simple math and figure out where the origin is in relation to our line. From looking at the picture it’s pretty obvious
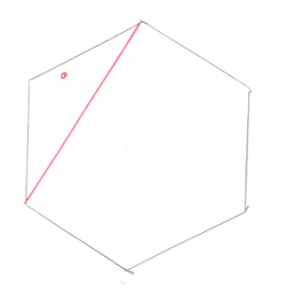
The origin is above the line. That arrow becomes our Support Vector and the next step is to find the point that is furthest along that Support Vector. Pretty easy to see that the top most point is the one we’re looking for. If you add that point to the existing line you get a Triangle
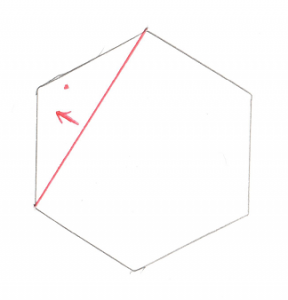
Now that’s all well and good, but there’s a problem, the origin isn’t inside that triangle. We can do some math to prove it and find out that the origin is to the left of the leftmost line. This means that the right most point is no longer of interest to us, so we can throw it away and we’ll find ourselves back to the case of a single line
And again, we want to figure out where the origin is in relation to the single line. Pretty obvious that it’s on the left side.
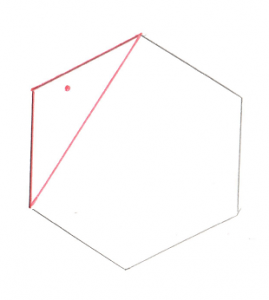
And just like before, that arrow becomes our Support Vector. And we want to find the point furthest along in that direction. And if we add that point to our existing line, we create a new triangle.
This new triangle contains the origin. Huzzah! Since a triangle inside the Minkowski Difference contains the origin, the original two shapes are intersecting, we have a collision.
If you are a bit unclear, why not have a look at another article explaining the same thing. I have to give the author credit for using sticks and clay to create a 3D representation of the GJK. Well done!
In the next post, we’ll take a look at the specifics of the algorithm and the code.
| << Angular Motion | Contents | GJK Part 2 >> |