Believe it or not, all of the Math we’ve been discussing up until now has been leading us to this point. Now we have enough knowledge to introduce the Coordinate_space. In the Dubious Engine, a Coordinate_space represents an object’s position and rotation. Given what we’ve learned about Vectors, Points, and Quaternions, I hope it’s not surprising to see the data in the class:
class Coordinate_space {
Point m_position;
Unit_quaternion m_rotation;
};
That’s all we need to describe where an object is, and which way it’s facing. Before we take a look at how all the pieces come together to move one of these things around, let’s discuss “handedness.”
Right Handed Coordinate Space
I’ve been purposefully glossing over this subject up until now because I thought it was too much detail. But now that we’re finalizing our Math section, it’s time to discuss the ambiguity in our Z axis. From your earliest Math classes dealing with X and Y axis you’ve probably been told that the X axis goes from left to right, by which I mean +100 is further to the right then -100. Likewise you probably see the Y axis as going up (ie +100 is higher up then -100). But what about the Z axis? Does it point out of your computer screen towards you, or from you into the screen? Well it turns out that both systems are equally valid, and different Math packages use one way or the other. It’s not a big deal to convert between them, but it’s definitely a lot simpler to pick one and stick with it. OpenGL and Bullet Physics both use a system where the positive Z axis points from your screen out to you (ie your nose is +100 and the area behind your screen is -100). I decided I wanted my coordinate space to match OpenGL so it would be easy to draw what I was building in my Physics Engine.
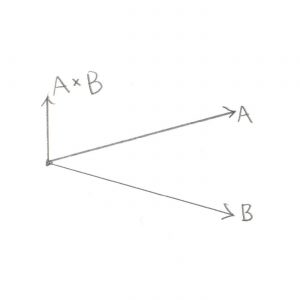
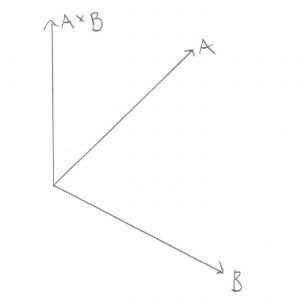
What’s this have to do with hands? Well to help us give a name to the two different ways of orienting your Z axis, someone came up with a way to illustrate the X, Y, and Z using your fingers. If you hold up your right hand and point your thumb along the +X Axis, and your index finger along the +Y Axis, you can then point your middle finger at your nose and call that the +Z Axis. This is a Right Handed Coordinate System. If you try to do the same thing with your left hand you’ll see that your middle finger points away from your nose, a Left Handed Coordinate System.
There’s one more hand trick that might even be more important when representing rotations using Axis and Angle. You may have noticed that up until now I’ve said that the Axis is the Vector you rotate around, and the Angle is the amount you rotate, but I never specified which direction to rotate. By using our hands we can finally answer that question. If you represent your Axis Vector as running along your thumb (the thumb nail is +100, palm is -100) then a positive rotation is the direction in which the rest of your fingers curl when you make a fist.
Let’s put all those bits together with an example. Let’s demonstrate a positive rotation around the +Z Axis using the Right Handed Coordinate System. Start by holding your right hand in front of your face with all of your fingers open and with your thumb pointing at your nose. Your thumb now represents the positive Z Axis. Curl your fingers into a fist, that is positive rotation. You should see your fingers curling counter clockwise. When you see information about a Right Hand Coordinate System online you’ll often see that positive rotation is counter clockwise.
If you’re trying that out and it’s not working as expected, re-read this and try again. It’s worth getting right because bugs in the direction of rotation are really hard to figure out. The more you understand it now, the easier your life will be.
Actions on a Coordinate_space
Turning our attention back to the Coordinate_space, let’s look at the functions it supports. At the core, it has some transform functions that serve to convert global Points and Vectors to local Points and Vectors, and vice versa. The usage of types makes these very transparent:
Vector transform( const Local_vector& v ) const; Local_vector transform( const Vector& v ) const; Point transform( const Local_point& p ) const; Local_point transform( const Point& p ) const;
The code that drives these is based on Quaternion magic, so I can’t pretend to understand everything about why it works, but I am comfortable that it does.
As you can see, there’s no need to specify in the function name what you’re transforming from and to, we just use the type system to do the right thing. This is another good argument for why a Vector and a Point should be different. Since Vectors have no position, the transform function simply rotates them. And since Points do have a position, the transform function rotates them and moves them. For example, if we have a Coordinate_space that is moved to (1,0,0) and rotated 90 degrees around (0,1,0), and we have a global point at (2,0,0), by now you should be able to reason that if we converted that Point into the Coordinate_space it would be at (0,0,1). Try out a bit of invisible knitting yourself, to see if you get the same result.
Aside from these helper type functions, a Coordinate_space has the usual translate and rotate things you’d expect. I won’t dwell on those, they do what you’d expect, they move and rotate the Coordinate_space. Their implementation is straight forward with the help of the transform functions.
The last function is one that I find myself using a lot, it’s this:
std::tuple<Unit_vector,Unit_vector,Unit_vector> get_axes() const;
This one returns the global X, Y, and Z axis for the Coordinate_space. How is that useful? Let’s say you’re flying in your space ship and you want to fire a laser. What direction is the laser going to go? Clearly it is going to fly straight out from the front of your ship. And what direction is straight out? Well that would be along the +Z Axis. So with this simple function it’s easy to grab the direction in which the laser should fly. In normal usage you would create a new Laser object, drop it into your game, and set it’s velocity to be a Vector of some magnitude (the longer the faster) directly along the +Z Axis that this function returns.
So there you have it, our long journey through the Math of the Dubious Engine is now complete. We have created simple ways to deal with Points, Vectors, Rotations, and Coordinate_spaces. Now we have enough tools at our disposal to go ahead and start talking about the point of this whole thing: Physics.
| << Using Types | Contents | Linear Motion >> |